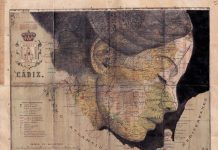
Một mặt cầu khi được khai triển thành một mặt phẳng luôn bị rách hay bị nhăn. Khi biểu diễn quả đất hình cầu lên tờ giấy phẳng, tất nhiên cũng xuất hiện những biến dạng. Những biến dạng này sẽ tạo ra các sai lệch mà ta sẽ lần lượt xét tới sau đây

Xem thêm: Đo vẽ nhà đất – khái niệm và dịch vụ đo vẽ nhà đất
1. Dẫn đến sai số khoảng cách trên bề mặt trái đất.
Xét hai điểm A và B cùng nằm trên mực thủy chuẩn của quả đất; khoảng cách d trên mặt đất được biểu diễn bằng bề dài cung AB. Nếu coi mặt thủy chuẩn là mặt phẳng thì khoảng cách giữa A và b là chiều dài tiếp tuyến AC = t. Sai số về khoảng cách do việc giả thiết mặt thủy chuẩn là mặt phẳng sẽ là:
Δd = t – d.
t = R.tgθ với θ = d/R.
Vậy Δd = R(tgθ – θ).
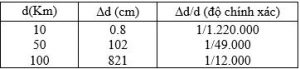
Tính gần đúng: Δd ≈ d.d.d/(3.R.R)
Thay R = 6371 km và cho d các giá trị khác nhau, ta sẽ có các giá trị Δd tương ứng được ghi trong bảng sau:
Trong thực tế đo đạc, với các công cụ hiện đại dùng để đo khoảng cách mà con người đang có, thì việc đo chiều dài chỉ đạt độ chính xác cao nhất là 1/1.000.000; do đó trong khu vực đo vẽ có bán kính dưới 10 km, ta có thể coi như mặt thủy chuẩn là mặt phẳng mà hoàn toàn không ảnh hưởng gì tới độ chính xác đo chiều dài.
2. Dẫn đến sai số về độ cao
Theo định nghĩa về độ cao thì hai điểm A và B có cùng độ cao vì chúng cùng nằm trên một mặt thủy chuẩn. Nhưng nếu giả thiết mặt thủy chuẩn qua A là một mặt phẳng (đó là tiếp tuyến At) thì người quan sát tại A sẽ thấy điểm C mà không thấy điểm B, đoạn BC = Δh chính là sai số về độ cao. Theo hình vẽ, ta có:
(R + Δh).(R + Δh)= R.R + t.t
Δh.Δh + 2R.Δh = t.t
Δh≈t.t/(2R+h’)
Vì h’ vô cùng nhỏ so với 2R nên có thể bỏ qua h’ ở mẫu số, coi t ≈ d, ta sẽ có:
Δh≈t.t/2R
Δ Với R = 6371 km, ta sẽ tính được Δh ứng với những khoảng cách d khác nhau (theo bảng dưới):
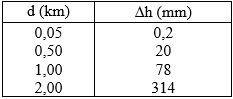
Do Δh tăng nhanh khi khoảng cách d tăng, hơn nữa do yêu cầu về độ chính xác trong đo độ cao khá cao nên ta phải xét đến ảnh hưởng của sai số này và tìm cách khắc phục. M ặt thủy chuẩn được dùng làm mặt chiếu, dùng phép chiếu xuyên tâm có tâm chiếu là tâm O của trái đất. Do khu vực đo vẽ nhỏ so với kích thước của quả đất nên các tia chiếu coi như song song với nhau và cùng vuông góc với (H). Vì thế hình chiếu abcde của đa giác ABCDE coi như hình chiếu lên mặt bằng (H), không bị biến dạng và rất giống như hình thực. các vĩ tuyến thành các đường nằm ngang song song nhưng không cách đều nhau: càng xa xích đạo các vĩ tuyến càng thưa dần, tức là biến dạng nhiều .
Nguồn : Bùi Quang Tuyến-Bài giảng trắc địa